Parte II

Nesta segunda parte serão apresentadas planificações de poliedros com elevada fracção de vértices planos, de um poliedro com o número mínimo de vértices não-planos, de um poliedro toroidal, de um poliedro pontualmente flexível, de um poliedro flexível e de dois sólidos com arestas curvas. É de relembrar que são vértices planos os do interior da planificação.

Como vimos no exemplo da figura 15 da parte I, em que há três vértices planos, a existência de concavidades pode facilitar bastante o desenho das planificações. Da figura 24 à 34, são vários os exemplos de poliedros cujas planificações possuem vértices planos.

Exercício 4   a) Desenhe uma planificação análoga à da figura 27 mas com quadrados. b) Desenhe planificações análogas às das figuras 29 ou 30 mas colando tetraedros às faces de um tetraedro ou colando pirâmides quadradas às faces de um cubo. c) Quantos tetraedros pode colar a um cuboctaedro (se quiser planificá-lo)? d) Desenhe a planificação do poliedro que se obtem colando pirâmides em todas as faces de um prisma pentagonal. e) Construa um poliedro análogo ao da figura 28 que tenha $3/20$ de vértices não-planos. f) Quantos poliedros diferentes é que se podem construir com a planificação 34?

Toro

Nesta secção será apresentado um processo para imaginar um poliedro toroidal e a sua planificação. Este processo pressupõe que é possível:

• Obter concavidades acentuadas usando apenas triângulos equiláteros (ver figura 35).
• Planificar vértices hiper-planos. São vértices hiper-planos aqueles cuja soma dos ângulos medidos sobre as faces à sua volta é superior a $2\pi$ rad (ver figura 36).
• Construir um poliedro toroidal com a mesma simetria que o disfenóide cuja planificação se encontra na figura 37.

A primeira parte do processo consiste em orientar um hexaedro (dois tetraedros colados) segundo a descrição da figura 38. A segunda parte consiste em unir quatro hexaedros, todos orientados de maneira análoga. A terceira parte consiste em adicionar vértices em localizações bem determinadas. Considere os vértices indicados na figura 38. Transforme C em C' por reflexão no plano ABD. Obtem-se

$$\overline{\mbox{CC'}} = \sqrt{4-\frac{242}{147-20\sqrt{15}}}$$

Se aproximar esta distância por $\sqrt{3}-1$ não cometerá um erro significativo e não precisará de régua para a medir pois a altura de dois triângulos equiláteros de lados unitários é $\sqrt{3}$ (ver figura 39).

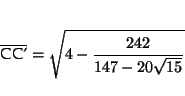
O erro que comete é da ordem de um e meio por cento. Os erros resultantes da espessura da cartolina e da montagem dos poliedros também são desta ordem e também não são, de maneira geral, significativos. No entanto há dois casos em que estes erros seriam inaceitáveis:

• Comparando a superfície específica de poliedros capazes de preencher o espaço [6].
• Tentando detectar flexibilidade. Este caso será estudado mais a fundo na secção seguinte.

Flexíveis

O poliedro da figura 40 poderá parecer flexível mas nem sequer é um poliedro. As faces só parecem encaixar umas nas outras porque a cartolina se deforma ligeiramente. As arestas têm comprimentos mal calculados. Um cálculo, feito com base na figura 41, indica que se deveria ter $r \approx 0.94414$ em vez de $r=1$. Por outro lado, a figura 42 indica que o poliedro é apenas pontualmente flexível [7]. Considera-se flexível todo o poliedro cujos ângulos interfaciais podem variar sem alterações da forma das faces. Foi demonstrado que estes poliedros têm volume constante [8], possuem arestas côncavas [9] e são flexíveis numa gama de ângulos interfaciais [10]. Um exemplo devido a Klaus Steffen da Universidade de Dusseldorf é o da figura 43.

Exercício 5   a) Verifique se é possível construir um poliedro toroidal cujas faces sejam todas triângulos equiláteros. b) Verifique se é possível construir um poliedro flexível apenas com as faces da figura 9 da parte I.

Arestas Curvas

Estudos de David Huffman [11] mostram que sólidos geométricos construidos a partir de folhas de papel podem possuir arestas curvas. Estas são mais difíceis de desenhar e vincar do que as rectas, no entanto, permitem a construção de sólidos bastante simples. É claro que estes sólidos não são poliedros mas podem ser construidos de maneira análoga, em particular, de maneira análoga aos poliedros com elevada fracção de vértices planos. Por exemplo, podemos adaptar a planificação 32 para obter a da figura 44. A forma das arestas curvas pode ser definida por uma expressão quadrática ou por um ``spline'' de Bézier sem inflexões. Se pegarmos num tetraedro e curvarmos uma aresta obtemos um sólido como aquele cuja planificação se encontra na figura 45.

Exercício 6   a) Modifique a planificação 25 por forma a possuir arestas curvas. b) Qual é a expressão mais simples que define a forma de arestas curvas quando planificadas? b) As arestas curvas pertencem sempre a um plano?

O autor agradece as críticas e as palavras de incentivo de Rui Rodrigues, Adérito Araújo, Eduardo Veloso e René Fonseca.