


Next: About this document ...
Up: Planificações de Poliedros e
Previous: Parte II
-
- 1
-
Peter Hilton, Jean Pedersen,
``Build Your Own Polyhedra'', Addison Wesley (1988).
- 2
-
Jean J. Pedersen, 1973, ``Plaited Platonic Puzzles'', College Math Journal
4 N
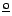 3, 22-37.
3, 22-37.
- 3
-
http://www.geom.umn.edu/docs/doyle/mpls/handouts/node19.html
- 4
-
Denis Weaire
(ed.) ``The Kelvin Problem, foam structures of minimal surface area'',
Taylor & Francis (1996) ISBN: 0-748-0632-8.
- 5
-
http://www.math.lsa.umich.edu/~hales/countdown/,
Tamas Hausel, Endre Makai, Andras Szucs, 2000, ``Inscribing cubes and
covering by rhombic dodecahedra via equivariant topology'' a publicar.
- 6
-
Ver o ficheiro kelvin-9tile-transp.html na
directoria
http://www.geom.umn.edu/graphics/pix/Special_Topics/Tilings/.
Denis Weaire, Robert Phelan, 1994, ``A
counterexample to Kelvin's conjecture on minimal surfaces''
Phil. Mag. Lett. 69 107-110.
- 7
-
Ver a página 161 do livro
``The Penguin Dictionary of Curious and Interesting Geometry'' de
David Wells (1991) que mostra o icosaedro ortogonal de Jessen,
também pontualmente flexível. Michael Goldberg, 1978, ``Unstable
Polyhedral Structures'', Mathematics Magazine 51 N
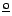 3,
165-170. Walter Wunderlich, 1979, ``Snapping and Shaky
Antiprisms'', Mathematics Magazine, 52 N
3,
165-170. Walter Wunderlich, 1979, ``Snapping and Shaky
Antiprisms'', Mathematics Magazine, 52 N
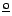 4, 235-236.
4, 235-236.
- 8
-
Robert Connelly, I. Sabitov, A. Walz, 1997, ``The Bellows
Conjecture'', em ``Contributions to Algebra and
Geometry'', 38 N
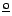 1, 1-10.
1, 1-10.
- 9
-
Cauchy, 1813, Second Mémoire, J. École
Polytechnique, 9 87, os poliedros convexos não podem ser
flexíveis.
- 10
-
Robert Connely, 1979, ``How to Build a Flexible
Polyhedral Surface'', em ``Geometric Topology'' Proceedings of the
1977 Georgia Topology Conference (Athens, Georgia), edit. James
C. Cantrell, Academic Press, 675. Robert Connely, 1979, ``The
Rigidity of Polyhedral Surfaces'', Mathematics Magazine, 52
N
 5, 275-283.
5, 275-283.
- 11
-
http://www.sgi.com/grafica/huffman/. David A. Huffman, 1976, ``Curvature and creases: A primer on paper'', IEEE
Trans. Comput. C-25, 1010-1019

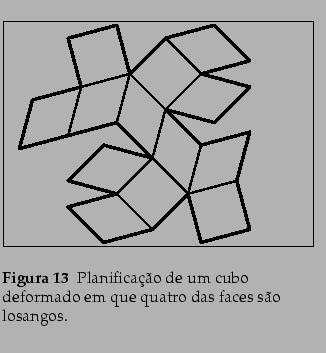
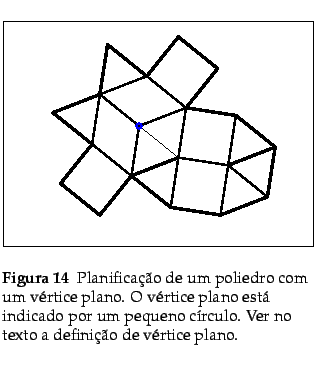
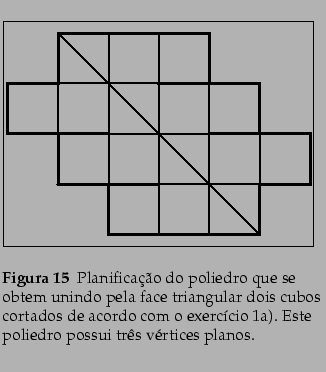
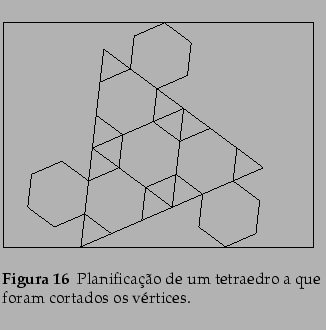

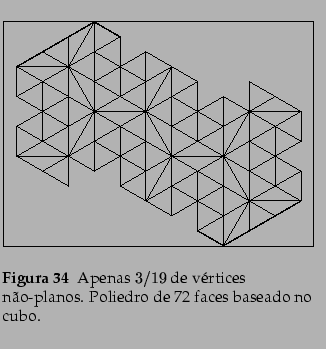
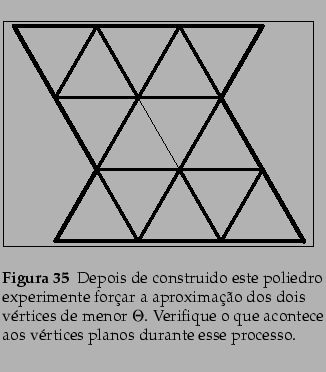
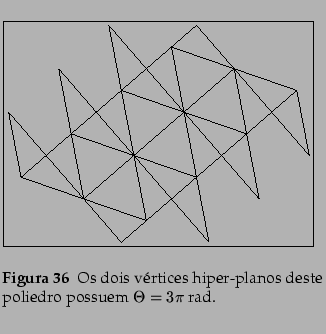
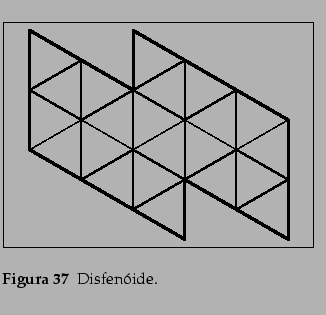
L. Nobre G.
2002-07-16