Parte I

Imaginar poliedros, conceber as suas planificações e construí-los é uma actividade capaz de exercitar e desenvolver, por exemplo:

• a capacidade de visualização,
• o interesse pela geometria e
• o gosto de experimentar.

Neste documento ensaia-se uma maneira de abordar esta actividade [1,2]. Assume-se que se aprende a conceber planificações por um processo de tentativa e erro. Imagina-se uma hipótese de planificação, verifica-se se permite montar o poliedro pretendido e volta-se ao princípio. Não há uma receita para determinar a boa planificação automaticamente. Cada poliedro pode ser planificado de muitas maneiras. A maneira que se acaba por escolher é a que melhor satisfaz os critérios pessoais da estética e da funcionalidade.

Começamos por uma pirâmide quadrangular, logo a seguir uma dupla pirâmide pentagonal e terminamos esta primeira parte com mais alguns exemplos de poliedros convexos, imaginando cortes e colagens.

Teoria

Comecemos por uma pirâmide de base quadrada (ver figura 1). Se os lados da base tiverem comprimento $l$ e se a pirâmide tiver altura $h$ então o comprimento das arestas que se unem no vértice superior é

$$x=\sqrt{\frac{1}{2}l^2+h^2}.$$

Munidos dos comprimentos de todas as arestas já podemos desenhar a planificação da pirâmide (ver figura 2). Agora recorta-se, dobra-se pelas arestas e usam-se as abas para colar. Aqui surge um problema: a última das faces a colar corta o acesso ao interior do poliedro e dificulta o pressionar da cola. Isto leva à utilização de cartolina muito fina por forma a tornar as dobras mais elásticas e exigirem menos pressão. Porém isto também torna o poliedro muito fácil de amachucar. É possível montar poliedros bastante rígidos aplicando a seguinte metodologia:

1. Em vez de abas desenhe as faces a que as abas colariam (ver figura 3).
2. Depois de vincar as arestas, coloque as faces alternadamente no lado exterior e no interior.
3. Use fita-cola para fixar a cartolina.

As planificações devem ser pensadas tendo em conta esta metodologia. Mesmo para melhorar a precisão dimensional deve reduzir-se o número médio de faces sobrepostas (ver figura 4). De maneira geral é boa política que as planificações possuam simetria central, que as faces com maior número de lados fiquem ao centro e que as faces encaixem como uma ``dentadura''. Por exemplo, uma dupla pirâmide de base pentagonal (ver figura 5) poderia ser planificada tal como se mostra na figura 6 ou então como na 7.

Notação

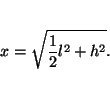
As linhas usadas no desenho das planificações devem ser interpretadas de acordo com o esquema da figura 8. Por outro lado, na figura 9 são descritos os tipos de faces usados. Todas as planificações são combinações deste conjunto de faces. Note-se ainda que só se consideram planificações de um único pedaço de cartolina.

Prática

Vejamos agora um cubo. Uma planificação possível é a que se apresenta na figura 10. Quando se deforma o cubo a planificação ressente-se (ver figura 11). A deformação aplicada consiste em afastar dois vértices que se encontrem sobre uma linha recta que contenha o centro do cubo.

Exercício 1   a) Suponha que corta o cubo unitário da figura 12 por um plano que contém A, B e C. Retire a parte que contém D e esqueça-a. Qual é a distância de E ao plano ABC? b) Cole um tetraedro de lados $\sqrt{2}$ à superfície de corte. Corte o que resta do cubo segundo os planos que contêm as faces expostas do tetraedro. Nestas condições a linha EF é cortada a que distância de F? c) Desenhe a respectiva planificação.

Introduzamos agora uma pequena modificação no poliedro da figura 11: vamos substituir duas faces por quadrados. Em princípio as duas faces a substituir não terão arestas em comum (ver figura 13). Agora se a substituição por quadrados tiver lugar em faces com uma aresta em comum somos forçados a dobrar losangos (ver figura 14).

Exercício 2   a) Verifique que os poliedros das figuras 11 e 13 têm o mesmo volume. b) Construa um poliedro que se possa obter cortando ao meio qualquer dos dois. c) Planifique os dois poliedros análogos aos das figuras 10 e 11 mas cujas faces são do tipo (g) na figura 9.

Definições

Concerteza reparou que ao recortar o poliedro da figura 14 a tesoura não atinge o vértice indicado. Isto quer dizer que se poupou uma aba. A dobragem ficou mais díficil mas a rigidez do poliedro foi aumentada. Os vértices a que a tesoura não chega serão, daqui em diante, denominados por vértices planos. Planos no sentido em que a cartolina cobre $2\pi$ rad à sua volta. Estes vértices são necessariamente extremos de uma ou mais arestas côncavas. Vários tipos de vértices podem ser definidos com base no ângulo $\Theta$ coberto pela cartolina à volta dos mesmos.

$$\Theta = \sum_{i=1}^{N_f} \theta_i$$

em que $N_f$ é o número de faces do poliedro que partilham um vértice e $\theta_i$ é o ângulo no canto da face $i$ que contém esse vértice.

Vértice plano:

$\Theta = 2\pi$ rad.

Vértice não-plano:

$\Theta \neq 2\pi$ rad.

Vértice hiper-plano:

$\Theta > 2\pi$ rad.

Descartes definiu o ``ângulo de defeito'' $\delta=2\pi-\Theta$. A soma de todos os ``ângulos de defeito'' de um poliedro é sempre $4\pi$. A demonstração envolve o teorema de Euler ($V+F=A+2$ em que $V$ é o número de vértices, $F$ é o número de faces e $A$ é o número de arestas) mas não será apresentada aqui [3].

Continuação da Prática

Regressemos ao cubo que foi cortado de acordo com o exercício 1a). Una, pela face triangular, dois iguais a esse (ver figura 15).

E agora regressemos ao início: a pirâmide da figura 1. Se se unirem duas pela base obtemos um octaedro. Os octaedros e os cubos são poliedros duais. Têm o mesmo número de arestas mas trocam os vértices por faces e vice-versa. Imagine o seguinte: pega num octaedro e corta os seis vértices a uma certa distância do centro sempre perpendicularmente aos eixos de simetria. São eixos de simetria as três linhas rectas que contêm o centro e um par de vértices. Imagine que começa por cortar muito pouco e que vai diminuindo gradualmente a distância ao centro. A certa altura as faces triangulares equiláteras do octaedro original transfomaram-se em hexágonos. Trata-se de um octaedro truncado, também conhecido por poliedro de Kelvin [4]. Não é possível obter uma planificação de acordo com o método descrito na Teoria porque sobra muito pouco espaço para as abas. Se fizer o mesmo com um tetraedro obtem espaço à justa (ver figura 16). Mas continuemos a cortar. Quando os hexágonos se tiverem reduzido a triângulos terá nas mãos um cuboctaedro (ver figura 17). Continuemos, finalmente chegamos ao cubo.

Voltemos a olhar para o octaedro. Quando colocado em cima da mesa vê-se uma faixa horizontal de triângulos (ver figura 18) alternadamente virados para cima e para baixo. A base pode ter qualquer forma. Quadrada por exemplo. Colemos a nossa pirâmide de partida a uma destas bases quadradas (ver figura 19). Mas repare: em vez de colar a pirâmide pode escavar uma pirâmide e a planificação é a mesma (ver figura 20).

Pegando num octaedro ou num cubo e cortando as arestas até as faces originais desaparecerem obtem-se o poliedro da figura 21 e 22. Trata-se do dodecaedro rômbico. É possível preencher completamente o espaço encaixando dodecaedros rômbicos uns nos outros. Os centros de massa dos dodecaedros rômbicos nessa situação formam uma rede cúbica de faces centradas que corresponde ao máximo empacotamento de esferas [5]. É de notar que os vértices de um cuboctaedro também formam uma rede cúbica de faces centradas.

Exercício 3   a) Considerando a analogia com o poliedro da figura 21 determine o ângulo (diedro) entre as faces sombreadas do poliedro cuja planificação se encontra na figura 23. b) Preencha o espaço apenas com cuboctaedros.